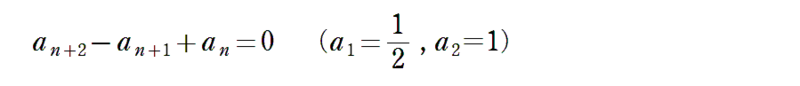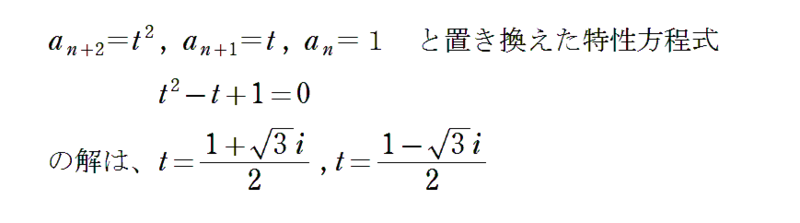隣接３項漸化式　特性方程式の解が虚数の場合は？

今年１月１０日の記事で、次のような漸化式を取り上げました。

一般項を求めようと、定石通りに「特性方程式」を解いてみたらなんと虚数解！想定外でしたね。

問題（福岡大学医学部の入試問題）自体は、第７項と第８項を求めるものですから、既知である初項と第２項を使って第３項を求め、次に第２項といま求めた第３項を使って第４項を求める。このように順次しりとり的に求めていけば、第７項が1/2、第８項は1、であると分かります。

実は、第７項は初項と、第８項は第２項と同じになっています。周期が６である循環的に同じ値をとる数列だったんです。

ですから、一般項をnの式で求めて、n=7,n=8を代入することはしなくてよかったんです。

では、一般項は求められないのか？　この不可解な特性方程式の虚数解に意味はないのか？という疑問が湧いてきますね。

求められなくはないですが、数学Ｂだけでなく数学III（ドモアブルの定理）やそれ以外の知識も少し必要です。

これを先ほどの一般項の式に代入してみましょう。

では、これが正しいか検算してみましょう。第７項と第８項でチェックします。

合ってました(^^)/　ヤレヤレ。

説明していない定理も天下り的に使っていますから、分かりにくかったかもしれません。なかなか大変でした！

入試問題では、こんな解法でしか解けない問題は出ませんね。順番にしりとり式に求めていけば、たいていどうにかなります。